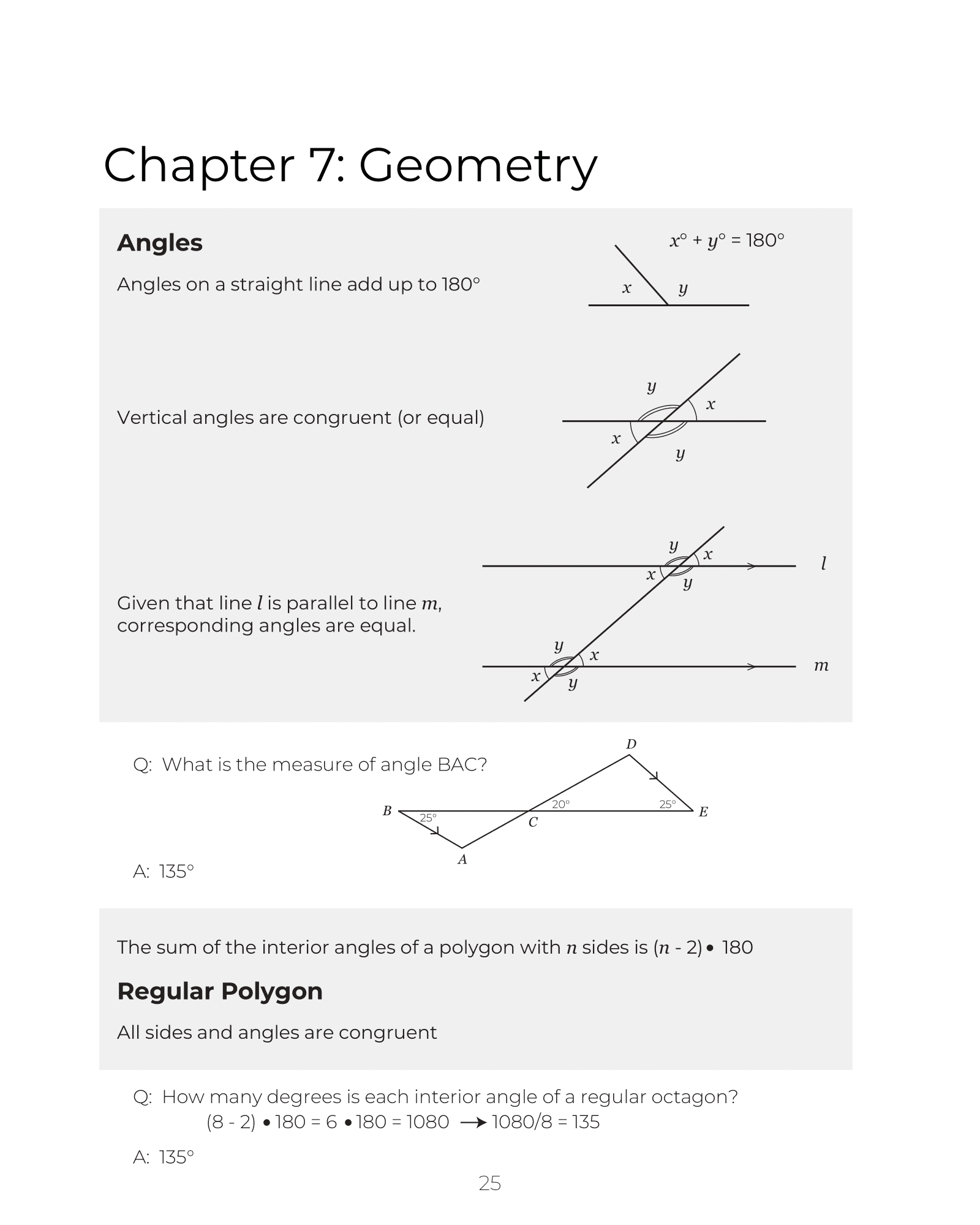
SAT Math · Deep Dive Guide
SAT Math Guide: Algebra, Circles, Trigonometry & Radians
This guide is built from real SAT practice questions and focuses on four topics that confuse a lot of students: algebra with substitution, circle equations, basic trigonometry, and radians / the unit circle. Work through the explanations and examples below, then apply what you learn in full-length SAT practice tests and targeted practice sessions. You can also drill specific problem types in the Study Share question bank and check your readiness with the SAT score calculator.
Who this is for: students aiming to move from the 500–600 range into the 650–750+ range on SAT Math by shoring up a few high-yield concepts.
SAT Algebra Basics: Substitution & Linear Equations
A large chunk of SAT Math is really about clean algebra. The test expects you to understand how variables stand in for numbers, how to substitute known values, and how to undo operations in the reverse order (using inverse operations).
Understanding substitution on the SAT
When the test tells you that a variable equals a number, you can replace that variable everywhere it appears. For example, suppose the question gives you the equation (x − 1) / 3 = k and then tells you that k = 3. Your first move is to substitute:
(x − 1) / 3 = 3
From here, solve using inverse operations:
- Undo division by 3 by multiplying both sides by 3: x − 1 = 9.
- Undo subtraction of 1 by adding 1 to both sides: x = 10.
The key rule: whatever you do to one side of the equation, you must do to the other. The SAT loves making you apply this rule systematically.
Translating word problems into equations
Many "verbal math" questions simply hide a basic linear equation. For example, imagine a problem that says:
"When 4 times a number x is added to 12, the result is 8. What number results when 2 times x is added to 7?"
Translate the first sentence into an equation:
12 + 4x = 8
Now solve step by step:
- Subtract 12 from both sides: 4x = -4.
- Divide both sides by 4: x = -1.
The question is not asking for x directly. Instead, it wants the value of 7 + 2x. Substitute x = -1:
7 + 2(−1) = 7 − 2 = 5
So the answer choice corresponding to 5 is correct. On the SAT, always check whether the question wants the value of the variable or the value of an expression involving that variable.
Equation of a Circle on the SAT
Circle questions can look intimidating, but most of them boil down to one core formula and a few simple ideas about completing the square.
The standard equation of a circle
(x − h)² + (y − k)² = r²
- (h, k) is the center of the circle.
- r is the radius.
- x and y are any point on the circle.
Converting from general form using completing the square
Many SAT questions present a circle in "general" form, such as:
2x² − 6x + 2y² + y = 45
To identify the center and radius, you need to convert this to standard form by completing the square.
- Make the squared coefficients 1. Divide everything by 2:x² − 3x + y² + (1/2)y = 45 / 2
- Group x-terms and y-terms.(x² − 3x) + (y² + (1/2)y) = 45 / 2
- Complete the square for each group. For x² − 3x, take half of −3 (which is −3/2) and square it: (−3/2)² = 9/4. For y² + (1/2)y, take half of 1/2 (which is 1/4) and square it: (1/4)² = 1/16. Add these to both sides:(x² − 3x + 9/4) + (y² + (1/2)y + 1/16) = 45 / 2 + 9/4 + 1/16
- Factor the perfect squares.(x − 3/2)² + (y + 1/4)² = 25
Now it's in standard form. The center is (3/2, −1/4) and the radius is √25 = 5.
Using the circle equation to read graphs
In other questions, the circle is already in standard form and you use the equation to sketch or interpret the graph quickly. For example:
(x − 6)² + (y + 5)² = 16
- Center: (6, −5)
- Radius: √16 = 4
Once you know the center and radius, you can draw the circle and reason about diameters, chords, and labeled points—often without doing heavy algebra.
Trigonometry on SAT Math: SOH CAH TOA & Cofunctions
Trigonometry shows up in a relatively small number of SAT questions but is very predictable. Almost everything you need comes from right triangles and the three primary trig ratios.

SOH CAH TOA: your trig cheat code
Sine = Opposite / Hypotenuse
Cosine = Adjacent / Hypotenuse
Tangent = Opposite / Adjacent
On the SAT, these ratios always refer to a right triangle. First identify the reference angle (not the right angle), then label the sides as opposite, adjacent, and hypotenuse relative to that angle.
Cofunction identities on the SAT
There is one trig identity that appears more than any other on the SAT:
cos(90° − x°) = sin(x°)
sin(90° − x°) = cos(x°)
These are called cofunction identities. They come from the fact that in a right triangle, the two acute angles sum to 90°, so the side opposite one angle is adjacent to the other.
Example: using cofunctions to avoid heavy trig
"In a right triangle, one angle measures x°. If sin x° = 4/5, what is cos(90° − x°)?"
Using the cofunction identity, cos(90° − x°) = sin(x°). You don't need to draw a triangle at all:
cos(90° − x°) = sin(x°) = 4/5
So the correct answer is 4/5. On test day, recognizing this identity can save you 30–45 seconds per question.
Radians and the Unit Circle on the SAT
Radians show up in only a few questions, but they can feel confusing if you're more comfortable with degrees. The good news: there are only a handful of facts you really need.

What is a radian?
Imagine wrapping the radius of a circle around its circumference. The length of one radius along the edge is 1 radian. It takes 2π such radii to go all the way around the circle.
- Full circle: 2π radians = 360°
- Half circle: π radians = 180°
- Quarter circle: π/2 radians = 90°
Quick degree–radian conversions
Use these conversion formulas:
- Degrees → radians: (degrees) × π / 180
- Radians → degrees: (radians) × 180 / π
Example: comparing a central angle to a full circle
"In a circle, a sector has central angle 5π/4 radians. What fraction of the circle's area does this sector represent?"
A full circle is 2π radians, so the fraction of the circle is:
(5π/4) ÷ 2π = (5π/4) × (1 / 2π) = 5 / 8
The sector covers 5/8 of the circle's area. This exact reasoning also works for arc length problems.
Example: using the unit circle to find a radian measure
A point A lies on a circle of radius 2 with coordinates (√3, 1). The center is at the origin. What is the measure of angle AOB in radians?
First, notice that the point (√3, 1) has distance 2 from the origin:
(√3)² + 1² = 3 + 1 = 4 = 2²
To compare with the unit circle, divide both coordinates by the radius 2. The corresponding point on the unit circle is:
(√3 / 2, 1 / 2)
On the unit circle, the point (√3/2, 1/2) corresponds to angle π/6. So the measure of angle AOB is π/6.
Example: converting a large degree measure to radians
"An angle measures 720°. It is written as aπ radians, where a is a constant. What is the value of a?"
Convert 720° to radians:
720° × (π / 180°) = 4π
So a = 4. You can also think of this as two full revolutions (since 360° × 2 = 720°), and each full revolution is 2π radians, giving 4π.
Key Formulas, Identities, and SAT Math Takeaways
Quick reference checklist
- Algebra substitution: plug in known values, then use inverse operations; answer may be an expression like 7 + 2x, not just x.
- Circle equations: (x − h)² + (y − k)² = r²; use completing the square to go from general form to standard form.
- SOH CAH TOA: memorize the ratios and always label sides relative to the reference angle, not the right angle.
- Cofunctions: cos(90° − x°) = sin(x°), sin(90° − x°) = cos(x°).
- Radians: full circle 2π, half π, quarter π/2; convert using π / 180 and 180 / π.
- Unit circle: memorize the coordinates for π/6, π/4, π/3, and their symmetric angles; x = cos θ, y = sin θ.
These four topics—algebra substitution, circle equations, basic trigonometry, and radians—show up again and again on SAT Math. Once you're comfortable with them, many medium and even hard questions become straightforward.
Use this guide side-by-side with the main SAT Math Reference Guide and Study Share's practice tests. The more you see these ideas in real questions, the more automatic they will become on test day.