SAT Math Reference Guide 2025
Master the SAT with our comprehensive visual study guide covering every essential math topic tested on the exam. This free resource provides clear diagrams, formulas, worked examples, and strategic tips to help you achieve your target score.
Our study guide breaks down complex concepts into digestible visual formats. Each section includes annotated diagrams, step-by-step examples, and key formulas you'll need on test day. When you're ready to apply what you've learned, try our full-length SAT practice tests or jump into targeted practice sessions to reinforce your understanding.
Pro Tip: Bookmark this page and review it regularly. The SAT math section tests your ability to recognize patterns and apply formulas quickly. Familiarizing yourself with these visual references will help you solve problems faster and more accurately on test day.
Numbers and Number Properties
Understanding number properties is fundamental to SAT success. The exam frequently tests your knowledge of integers, rational and irrational numbers, prime factorization, and number operations. Master these concepts early, as they appear throughout both the calculator and no-calculator sections.
Key topics include: identifying even and odd numbers, understanding place values, recognizing rational vs. irrational numbers, working with undefined expressions and zero rules, prime factorization, finding greatest common factors (GCF) and least common multiples (LCM), and applying number properties to solve complex problems.

The first page covers essential integer properties. Understanding even and odd number rules helps you quickly eliminate answer choices. For example, the sum of two even numbers is always even, and the product of an even and odd number is always even. Place value knowledge is crucial for working with large numbers and decimal operations.

Distinguishing between rational and irrational numbers is essential. Rational numbers can be expressed as fractions (p/q where p and q are integers), while irrational numbers cannot. Common irrational numbers include √2, π, and e. Understanding when expressions are undefined (like division by zero) helps you identify impossible answer choices quickly.

Prime factorization is a powerful tool for finding GCF and LCM efficiently. The GCF is the product of common prime factors raised to their lowest power, while the LCM is the product of all prime factors raised to their highest power. These concepts frequently appear in word problems involving ratios, rates, and repeating patterns.
Algebra and Polynomials
Algebra forms the backbone of the SAT math section, appearing in approximately 35% of all questions. Master polynomial operations, factoring techniques, and algebraic manipulation to build a strong foundation. Understanding how to work with variables, coefficients, and constants is essential for solving equations and inequalities efficiently.
Polynomials are expressions with multiple terms, and the SAT tests your ability to add, subtract, multiply, and factor them. Key skills include recognizing polynomial patterns, applying the distributive property, and using factoring techniques like grouping, difference of squares, and perfect square trinomials.

This page provides a comprehensive overview of polynomial operations and quadratic equations. Understanding the structure of polynomials—terms, coefficients, degrees, and leading coefficients—helps you identify patterns and solve problems more efficiently. Quadratic equations, which appear frequently on the SAT, can be solved using multiple methods including factoring, completing the square, and the quadratic formula.

Quadratic functions graph as parabolas, and understanding their key features is crucial. The vertex form, y = a(x-h)² + k, immediately reveals the vertex (h, k) and the direction of opening (up if a > 0, down if a < 0). The standard form, y = ax² + bx + c, helps identify the y-intercept (c) and can be used with the quadratic formula. The factored form reveals the x-intercepts (roots) directly.

Completing the square is a powerful technique for converting quadratic equations to vertex form and solving them. The discriminant, b² - 4ac, tells you about the nature of the roots: positive discriminant means two real roots, zero means one repeated root, and negative means two complex roots. This information helps you quickly determine if a quadratic equation has real solutions.

Understanding how parameters affect graphs is essential for interpreting function transformations. Changes to the coefficient 'a' affect the width and direction of parabolas, while changes to 'h' and 'k' shift the graph horizontally and vertically. Recognizing these transformations helps you match equations to graphs and solve problems involving function behavior.
Exponential and Linear Growth
Growth models are among the most frequently tested concepts on the SAT, appearing in word problems involving population growth, compound interest, radioactive decay, and more. Understanding the difference between linear and exponential growth is crucial for interpreting real-world scenarios and solving related problems.
Linear growth follows a constant rate of change, represented by y = mx + b, where m is the constant rate. Exponential growth follows a constant percentage rate, represented by y = a(1 + r)ᵗ or y = aeʳᵗ, where r is the growth rate. Exponential functions grow much faster than linear functions over time, which is why they're used to model phenomena like compound interest and population growth.

This visual guide demonstrates the key differences between linear and exponential models. Linear functions create straight lines when graphed, while exponential functions create curves that increase (or decrease) at an accelerating rate. Recognizing these patterns helps you identify the correct model for word problems and interpret graphs accurately. Pay special attention to the initial value (y-intercept) and growth rate, as these determine the function's behavior.
Functions and Function Operations
Functions are central to SAT math, appearing in approximately 30% of questions. A function is a relationship where each input (x-value) produces exactly one output (y-value). Understanding function notation, evaluating functions, and working with composite functions are essential skills for SAT success.
Key function concepts include: function notation (f(x)), evaluating functions at specific values, finding domain and range, composing functions (f(g(x))), and interpreting function graphs. The SAT also frequently tests distance-rate-time problems and proportional relationships, which can be modeled as functions.

This comprehensive page covers multiple function-related topics. When evaluating functions, substitute the given value for x and simplify. For composite functions, work from the inside out: first evaluate the inner function, then use that result as the input for the outer function. Distance-rate-time problems use the formula d = rt, which can be rearranged to solve for any variable. Proportions are solved using cross-multiplication, a technique that appears frequently in SAT word problems.
Polynomial Equations
Polynomial equations require matching coefficients when two polynomials are equal. This technique is essential for solving problems where you need to find unknown coefficients or determine if two expressions are equivalent. The SAT frequently tests this skill in problems involving polynomial identities and equation solving.

When two polynomials are equal, their corresponding coefficients must be equal. This principle allows you to set up systems of equations to solve for unknown coefficients. For example, if ax² + bx + c = 3x² + 5x - 2, then a = 3, b = 5, and c = -2. This technique is particularly useful for problems involving polynomial division, partial fractions, and polynomial identities.
Rational Functions and Asymptotes
Rational functions are ratios of polynomials, written as f(x) = P(x)/Q(x). Understanding their behavior, particularly asymptotes, is crucial for interpreting graphs and solving related problems. Asymptotes are lines that the graph approaches but never touches, and they provide important information about function behavior.
Vertical asymptotes occur where the denominator equals zero (and the numerator doesn't also equal zero at that point). Horizontal asymptotes describe the function' behavior as x approaches positive or negative infinity. The degree of the numerator and denominator polynomials determines the horizontal asymptote's location.

This visual guide demonstrates how to identify and interpret asymptotes. To find vertical asymptotes, set the denominator equal to zero and solve. For horizontal asymptotes, compare the degrees of the numerator and denominator: if the denominator's degree is greater, the horizontal asymptote is y = 0; if the degrees are equal, it's the ratio of leading coefficients; if the numerator's degree is greater, there's no horizontal asymptote (but there may be an oblique asymptote).
Trigonometry
Trigonometry appears in approximately 10-15% of SAT math questions, primarily in the context of right triangles and the unit circle. Mastering the basic trigonometric ratios (sine, cosine, tangent) and their relationships is essential for solving geometry problems involving angles and side lengths.
The mnemonic SOH CAH TOA helps remember the three primary trigonometric ratios: Sine = Opposite/Hypotenuse, Cosine = Adjacent/Hypotenuse, and Tangent = Opposite/Adjacent. Understanding these ratios allows you to solve for missing sides or angles in right triangles. Trigonometric identities, such as sin²θ + cos²θ = 1, are also frequently tested.

This page provides a comprehensive overview of trigonometric ratios and key identities. The SOH CAH TOA mnemonic is your best friend for right triangle problems. Remember to identify the reference angle first, then label the sides as opposite, adjacent, and hypotenuse relative to that angle. The Pythagorean identity (sin²θ + cos²θ = 1) is particularly useful for problems where you know one trigonometric ratio and need to find another.

Understanding the unit circle and quadrant relationships is crucial for solving trigonometry problems. The coordinate plane is divided into four quadrants, and the signs of sine and cosine depend on the quadrant: Quadrant I (both positive), Quadrant II (sine positive, cosine negative), Quadrant III (both negative), Quadrant IV (sine negative, cosine positive). Converting between degrees and radians is also essential: 180° = π radians, so to convert degrees to radians multiply by π/180, and to convert radians to degrees multiply by 180/π.
Coordinate Geometry
Coordinate geometry combines algebra and geometry, allowing you to solve geometric problems using equations and coordinates. This topic appears in approximately 20% of SAT math questions, making it one of the most important areas to master. Understanding lines, slopes, distances, and systems of equations is essential.
Key concepts include: slope-intercept form (y = mx + b), point-slope form (y - y₁ = m(x - x₁)), standard form (Ax + By = C), parallel and perpendicular lines, distance formula, midpoint formula, and solving systems of linear equations. These tools allow you to analyze geometric relationships algebraically.

This page covers the fundamental forms of linear equations. Slope-intercept form (y = mx + b) immediately reveals the slope (m) and y-intercept (b). Point-slope form is useful when you know a point and the slope. Parallel lines have equal slopes, while perpendicular lines have slopes that are negative reciprocals (m₁ × m₂ = -1). Understanding these relationships helps you quickly identify line equations and solve problems involving line intersections.

The distance formula, √[(x₂ - x₁)² + (y₂ - y₁)²], is derived from the Pythagorean theorem and calculates the distance between two points. The midpoint formula, ((x₁ + x₂)/2, (y₁ + y₂)/2), finds the point exactly halfway between two points. These formulas are essential for solving problems involving line segments, circles, and geometric shapes on the coordinate plane. Angle bisection problems often require understanding how to find points that divide angles or line segments proportionally.

Systems of linear equations can be solved using substitution or elimination. Substitution works well when one variable is already isolated. Elimination involves adding or subtracting equations to eliminate a variable. Both methods are equally valid; choose based on which seems more straightforward for the given problem. Systems frequently appear in word problems involving two variables, such as mixture problems, rate problems, and problems involving two unknown quantities.
Arithmetic Operations
Strong arithmetic skills form the foundation for all SAT math success. While calculators are allowed on part of the exam, understanding exponent rules, square root properties, and fraction operations helps you work more efficiently and catch errors. These fundamental skills appear throughout the test, often embedded in more complex problems.

Key exponent rules include: multiplying powers (add exponents), dividing powers (subtract exponents), power of a power (multiply exponents), and negative exponents (reciprocal). Square root properties include: √(ab) = √a × √b, √(a/b) = √a/√b, and (√a)² = a. Cross multiplication is essential for solving proportions and rational equations. Mastering these rules allows you to simplify expressions quickly and accurately.
Inequalities
Inequalities appear frequently on the SAT, testing your ability to solve and graph inequality relationships. Understanding how to manipulate inequalities (remembering to flip the sign when multiplying or dividing by a negative number) is crucial. Complex inequalities involve multiple conditions, while absolute value inequalities require considering both positive and negative cases.

When solving inequalities, treat them like equations but remember to flip the inequality sign when multiplying or dividing by a negative number. For absolute value inequalities like |x| < a, this means -a < x < a. For |x| > a, this means x < -a or x > a. Graphing inequalities on a number line helps visualize solution sets, with open circles for strict inequalities (< or >) and closed circles for inclusive inequalities (≤ or ≥).
Percents and Absolute Value
Percent problems are among the most common word problem types on the SAT, appearing in contexts like discounts, interest rates, population changes, and probability. Understanding percent change formulas and how to convert between percents, decimals, and fractions is essential. Absolute value equations test your ability to consider both positive and negative cases when solving.

For percent problems, remember: percent = (part/whole) × 100. Percent change = [(new - old)/old] × 100. When solving absolute value equations like |x| = a, consider both x = a and x = -a. For absolute value inequalities, remember the two-case approach: |x| < a means -a < x < a, while |x| > a means x < -a or x > a. These concepts frequently appear in word problems involving distance, error margins, and real-world scenarios.
Data and Statistics
Statistics and data analysis questions appear in approximately 15-20% of SAT math problems. These questions test your ability to interpret data, calculate measures of central tendency, understand probability, and analyze statistical measures. The digital SAT places particular emphasis on data literacy and real-world applications of statistics.
Key statistical concepts include: mean (average), median (middle value), mode (most frequent value), range, standard deviation, quartiles, and percentiles. Understanding when to use each measure helps you interpret data correctly. Probability problems test your ability to calculate the likelihood of events, often using combinations and permutations.

The mean (average) is calculated by summing all values and dividing by the count. The median is the middle value when data is ordered, or the average of the two middle values for even-numbered sets. The mode is the most frequently occurring value. Understanding which measure to use depends on the data: mean is sensitive to outliers, median is robust to outliers, and mode is useful for categorical data. The SAT frequently asks you to identify how these measures change when data is modified.

Probability = (favorable outcomes)/(total possible outcomes). For independent events, multiply probabilities. For mutually exclusive events, add probabilities. The complement rule states P(not A) = 1 - P(A). Understanding these rules helps you solve probability problems involving dice, cards, selections, and real-world scenarios. The SAT often tests conditional probability and probability involving "and" vs. "or" scenarios.

Advanced statistical concepts include margin of error (the range of uncertainty in a measurement), confidence intervals (ranges that likely contain the true value), and box plots (visual representations showing quartiles, median, and outliers). Box plots display the minimum, first quartile (Q1), median, third quartile (Q3), and maximum, helping you quickly identify the distribution's shape and identify outliers. Understanding these concepts is essential for interpreting data visualizations and statistical summaries on the SAT.
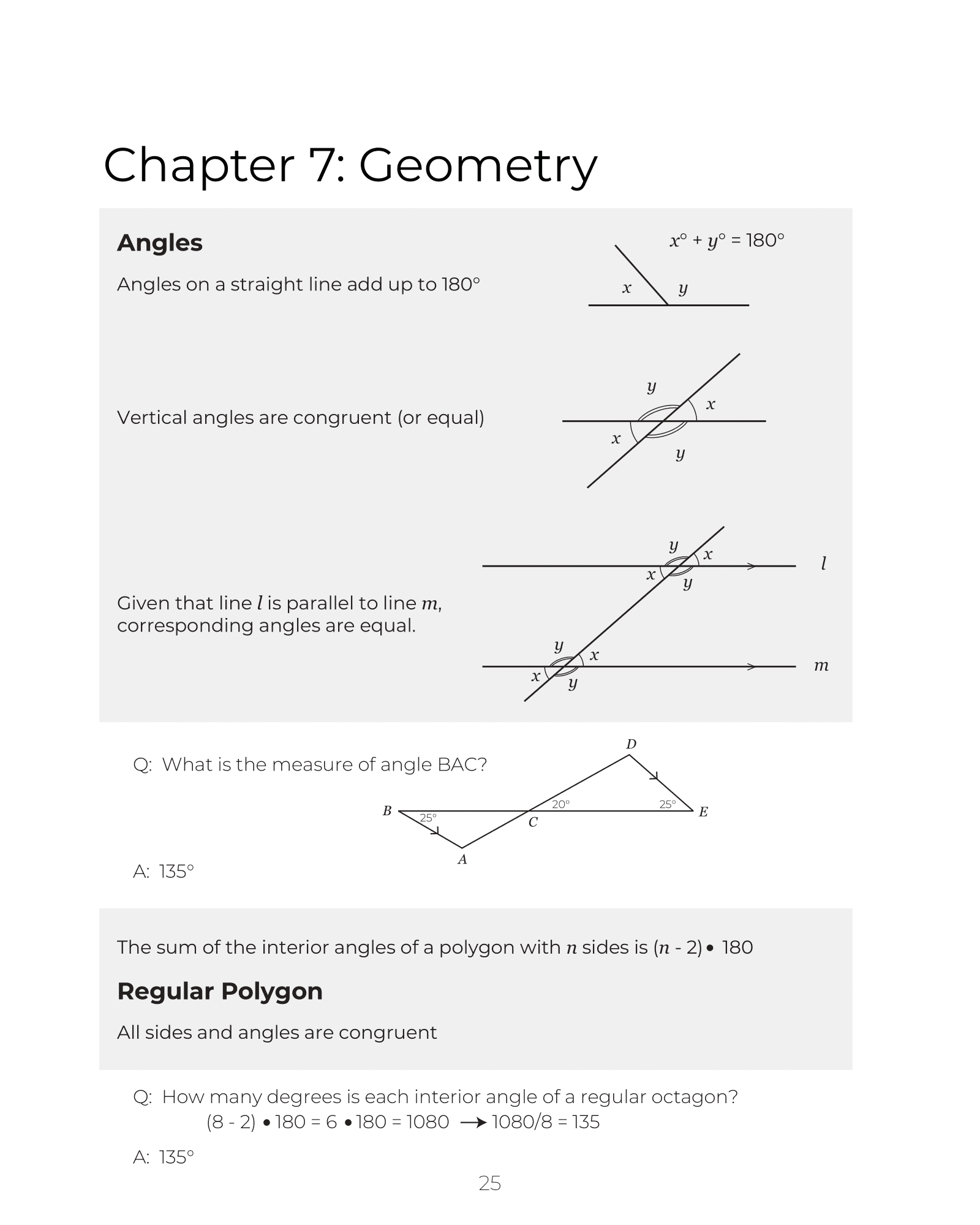
Geometry Fundamentals
Geometry questions account for approximately 15-20% of SAT math problems, testing your understanding of angles, polygons, area, perimeter, and spatial relationships. Mastering angle relationships, polygon properties, and geometric formulas is essential for success on these questions.

Key angle relationships include: complementary angles (sum to 90°), supplementary angles (sum to 180°), vertical angles (equal), and corresponding angles in parallel lines. The sum of interior angles in an n-sided polygon is (n-2) × 180°. Understanding these relationships helps you solve problems involving angle measures, parallel lines, and polygon properties quickly and accurately.
Circles
Circle problems are common on the SAT, testing your knowledge of area, circumference, arc length, and circle equations. Understanding the relationship between radius, diameter, and circumference, as well as how to work with circle equations in coordinate geometry, is essential.
Key circle formulas: Area = πr², Circumference = 2πr = πd (where d is diameter). The standard form of a circle equation is (x-h)² + (y-k)² = r², where (h, k) is the center and r is the radius. Understanding these formulas allows you to solve problems involving circle measurements, inscribed shapes, and coordinate geometry problems involving circles.

When given a circle equation in expanded form (x² + y² + Dx + Ey + F = 0), you can use completing the square to convert it to standard form. This reveals the center and radius directly. Group x-terms and y-terms separately, complete the square for each group, and simplify. This technique is essential for identifying circle properties from equations and solving coordinate geometry problems.
Arcs and Sectors
Arc length and sector area problems frequently appear on the SAT, often in the context of circles with central angles. Understanding the proportional relationship between angles and arc lengths/sector areas is key to solving these problems efficiently.

Arc length and sector area are proportional to the central angle. Arc length = (θ/360°) × 2πr, and sector area = (θ/360°) × πr², where θ is the central angle in degrees. Alternatively, if working in radians: arc length = rθ and sector area = (1/2)r²θ. The key insight is that these measures are fractions of the full circle, determined by the ratio of the central angle to 360° (or 2π radians).
Tangents to Circles
A tangent to a circle is a line that touches the circle at exactly one point. The key property is that a tangent is perpendicular to the radius at the point of tangency, forming a right angle. This relationship is frequently used in SAT problems involving circles and lines.

The fundamental property of tangents states that a tangent line is perpendicular to the radius drawn to the point of tangency. This creates a right angle, which allows you to use the Pythagorean theorem and right triangle trigonometry to solve problems. When a line is tangent to a circle, the distance from the circle's center to the line equals the radius. This property is essential for solving problems involving tangent lines, inscribed angles, and circle-line intersections.
Triangles
Triangles are the most common geometric shape on the SAT, appearing in approximately 10-15% of geometry questions. Understanding triangle properties, special triangles, and triangle relationships is essential for solving a wide variety of problems.

Key triangle properties: the sum of interior angles is always 180°, the exterior angle equals the sum of the two remote interior angles, and the triangle inequality theorem states that the sum of any two sides must be greater than the third side. Isosceles triangles have two equal sides and two equal base angles. Equilateral triangles have all sides and angles equal (60° each). Understanding these properties helps you identify triangle types and solve for missing angles and sides.

Special right triangles have fixed side ratios that you should memorize. The 45-45-90 triangle has sides in the ratio 1:1:√2, while the 30-60-90 triangle has sides in the ratio 1:√3:2. These ratios allow you to quickly find side lengths without using the Pythagorean theorem or trigonometry. Recognizing these special triangles in problems saves significant time and reduces calculation errors. The SAT frequently uses these triangles in problems involving geometric shapes, coordinate geometry, and trigonometry.
Similarity and Proportional Shapes
Similar triangles have the same shape but different sizes, with corresponding angles equal and corresponding sides proportional. Understanding similarity allows you to solve for unknown side lengths using proportions, which is a powerful technique for solving complex geometry problems.

For similar triangles, the ratio of corresponding sides is constant. If triangles ABC and DEF are similar, then AB/DE = BC/EF = AC/DF. This proportional relationship allows you to set up equations to solve for unknown side lengths. Common similarity scenarios include triangles with parallel lines, triangles sharing an angle, and triangles formed by altitudes or medians. Setting up and solving these proportions is a frequent task on the SAT geometry section.
Triangle Congruence Theorems
Congruent triangles are identical in shape and size, with all corresponding sides and angles equal. The five congruence theorems (SSS, SAS, ASA, AAS, and HL) provide conditions under which triangles are guaranteed to be congruent. Understanding these theorems helps you prove triangle congruence and solve related problems.

The five congruence theorems are: SSS (Side-Side-Side), SAS (Side-Angle-Side), ASA (Angle-Side-Angle), AAS (Angle-Angle-Side), and HL (Hypotenuse-Leg, for right triangles only). These theorems state that if the specified parts of two triangles are equal, then the triangles are congruent. Note that SSA (Side-Side-Angle) is NOT a valid congruence theorem, as it can produce two different triangles (the ambiguous case). Understanding these theorems helps you identify when triangles are congruent and use that information to solve for unknown angles and sides.

Ready to Put Your Knowledge to the Test?
Now that you've reviewed all the essential SAT math concepts, it's time to apply what you've learned. Practice is the key to SAT success, and we offer comprehensive resources to help you achieve your target score.
Study Tips for SAT Math Success
- •Review regularly: Bookmark this page and review it weekly. Familiarity with formulas and concepts reduces test-day anxiety.
- •Practice with purpose: Focus on your weak areas. Use our diagnostic tests to identify topics that need more attention.
- •Time management: The SAT math section is timed. Practice working efficiently while maintaining accuracy.
- •Understand, don't memorize: While formulas are important, understanding when and how to apply them is crucial.
- •Check your work: Use the calculator strategically, but don't rely on it for simple arithmetic. Mental math saves time.
About This SAT Math Reference Guide
This comprehensive SAT study guide is designed to help students master all essential math concepts tested on the SAT. These visual reference sheets provide clear explanations, worked examples, and key formulas you'll need on test day.
The SAT math section tests your ability to apply mathematical concepts to solve real-world problems. Success requires both conceptual understanding and procedural fluency. This guide helps you develop both by providing visual representations of abstract concepts and step-by-step examples of problem-solving techniques.
Remember, consistent practice is the most important factor in SAT success. Use this guide as a reference while working through practice problems, and return to it regularly to reinforce your understanding. Combined with our full-length practice tests and targeted practice sessions, this guide provides everything you need to achieve your target SAT score.